
Unfortunately, that source isn't readily viewable online (all I found was what appears to be a German version, at Berichte der Bunsengesellschaft für physikalische Chemie 1990, 94 (1), 93–93 (It's behind a paywall.) But if you could get your hands on it (interlibrary loan, say), it should contain a detailed description of how the values were actually calculated.įWIW, here's a link showing how standard molar entropies might be calculated (but I don't know if the procedure described here is what is used to determine the official CODATA values): Standard Molar Entropy of Solid Aluminum Oxide, Comments to Tandy Grubbs, Stetson University ( via the Internet Archive).Įssentially, it mentions using the Debye extrapolation I mentioned in an earlier comment up to $\approx\pu$, the fact that the system is locked into only one microstate (even if it's not a perfect crystal) gives it zero entropy. A., CODATA Key Values for Thermodynamics, Hemisphere Publishing Corp., New York, 1989. Here's a link to the official CODATA site showing the values:Ĭox, J.
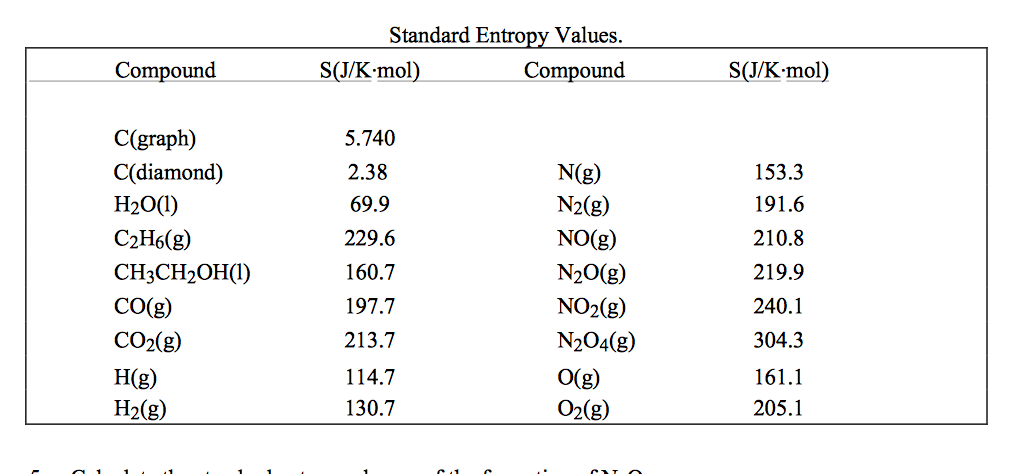
Not quite an answer, but too long for a comment: Because the entropy of a substance depends on the amount of substance, the pressure, and the temperature, it is convenient to describe the entropy of a substance in terms of S m, its standard molar entropy, i.e., as the entropy of 1 mol of substance at the standard pressure of 1 atm (101.3 kPa) and given temperature. What is the precise definition (preferably with reference) of standard molar entropy? 15.4 ( a ) At what temperature is the standard molar entropy of helium.
#STANDARD MOLAR ENTROPY HOW TO#
Most of the following issues will be covered by the exact definition, but to be more elaborate, these immediately come to my mind: what exactly is the standard state for each element? Do all elements form a perfect crystal at 0 K, and how can we prove this? Should I think of the third law (zero entropy at zero kelvin) as being a definition that sets an otherwise arbitrary baseline, or can it be proven that the quantum mechanical von Neumann entropy really is zero for pure elements at 0 K?Īn internet search turned up plenty of information about the values of standard molar entropy for various compounds and how to use them, but I wasn't able to find a resource with a detailed description of its definition. to the standard molar entropy at 298 K of ( a ) H2O ( g ), ( b ) CO2 ( g ). However, I'm not even sure that's exactly correct, and there are a lot of details that need to be filled in if it is right. Then, for the compound of interest, calculate and/or measure the entropy difference between the compound and its constituent elements at 0 K. Use this value, together with Boltzmanns equation, to determine the number of microstates. My recollection from a long time ago is that it goes roughly like this:įor each element, assume that its entropy goes to zero at 0 kelvin when it's in some standard state The standard molar entropy of H2(g) is S 130.7Jmol1K1 at 298K.

I understand what the standard molar entropy is, and how to use it in calculations, but I'm interested in understanding exactly how it's defined and measured.


 0 kommentar(er)
0 kommentar(er)
